隐式曲面
隐式曲面
# 隐式曲面
Owner: -QVQ-
表示衔接处光滑的物体,没有面拼接是它的优点
参数曲面,如Bezier曲面、B样条曲面、NURBS曲面等。参数曲面在造型和动画设计中取得了非常大 的成功,很多造型和动画系统都是基于 NURBS曲面的。
多边形网格(Polygon Mesh) 细分曲面(Subdivision Surface) 隐式曲面(Implicit surface, level set)
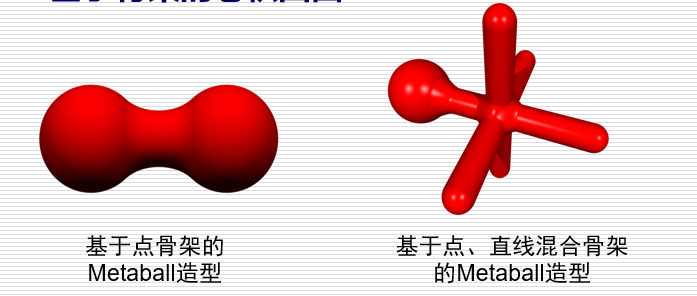
元球造型技术(Metaball)
起因:参数曲面在表现人体的肌肉、器官,液体等可 变形和可变拓扑场景的造型和动画等方面比较 困难,这促使人们寻找一种新的造型工具。
元球相互靠近到一定距离产生变形,再进一步靠近时则 融合成光滑表面。
以两个元球为例,元球靠近时的变形过程如左图所示。
以前用参数曲面做,但其交互性弱,现在人工智能让隐式曲面公式简单

很适合表示可变形和可变拓扑的物体,因而对 动画非常有用(如morphing)

像点、云
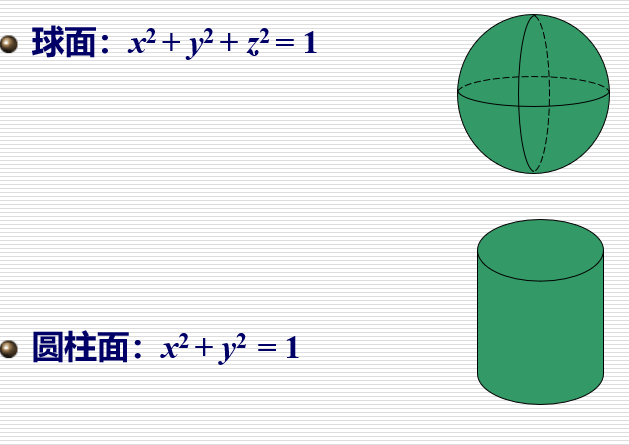
R3中的隐式曲面表示为:
三维空间中的一个二维曲面(二维流形) f (x, y, z)称为隐式函数:数学表达式或过程定义的函数 当f (x, y, z)为多项式函数时,隐式曲面称为代数曲面
举例:
与参数曲面相比,隐式曲面的不足
- 隐式曲面表示不直观,难以进行外形的交互修改。NURBS曲面的外形控制手段非常直观
- 隐式曲面通常没有边界,而NURBS曲面具有显式的边界
- 隐式曲面难以直接进行显示(隐式曲面全是方程的解),而NURBS曲面则可以借助于剖分算法,对逼近多边形表示进行绘制
与参数曲面(NURBS)相比,隐式曲面的优点
- (表示更多现状)隐式曲面可以表示具有复杂拓扑的形状,NURBS曲面只能表示拓扑等价于矩形的四边曲面
- (不需要光滑拼接)NURBS曲面表示非退化封闭光滑曲面时,需要光滑拼接
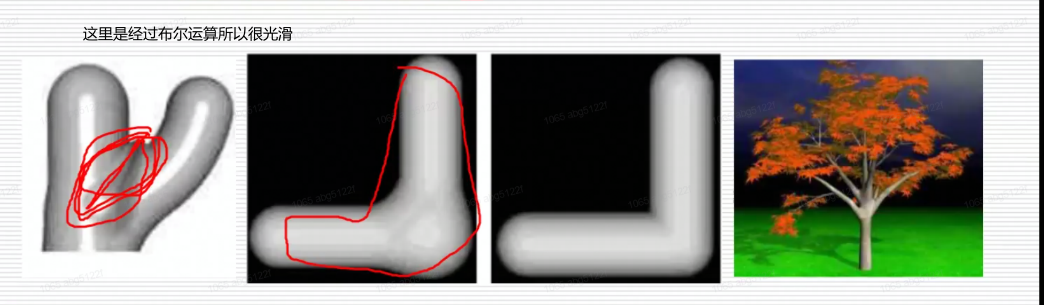
- (易于运算)隐式曲面比NURBS曲面更适合于进行布尔运算、光线跟踪、点集判断等
隐式曲面与参数曲面的相互转化
隐式化:
从参数曲面到隐式曲面 消除NURBS曲面的两个参数(u, v)得到其隐式表示 参数化:从隐式曲面到参数曲面 并非所有的隐式曲面都可以参数化 对于非退化的二次代数曲面和具有一个奇异点的三次代数曲面,可以进行有理多项式参数化
图形学中常用的隐式曲面造型技术
基于骨架的隐式曲面造型 基于点、线和面骨架的Metaball方法 基于骨架的卷积曲面
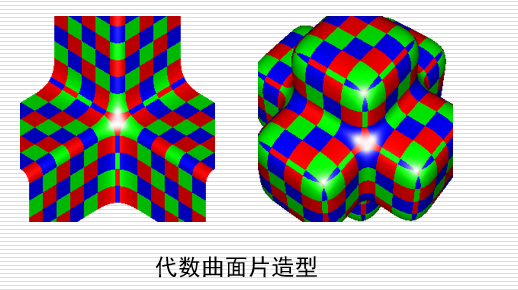
代数曲面片造型技术,包括二次代数曲面、A-Patch方法等
隐式曲面的显示
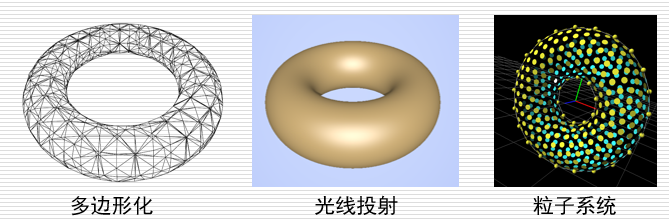
多边形化:用平面多边形逼近隐式曲面(Marching Cube方法)
光线跟踪:生成高质量的图像(求交点在交点上渲染,不需要像另外两个一样需要先构建3D再渲染)
粒子系统:在隐式曲面上均匀布撒粒子