 物体表示
物体表示
# 物体表示
Owner: -QVQ-
建模坐标系和世界坐标系


几何场景:定义在一个世界坐标系中,由许多物体组成
建模坐标系
选择空间坐标系,使得几何物体的表示最简单。该坐标系称为建模坐标系
世界坐标系
在建模坐标系中而不是在世界坐标系中直接表示物体的优势
1表示形式简洁 2在同一几何场景中,一个物体可能会多次出现,它们可以通过复制加变换的方式得到:标准体素“+”变换“=”新的物体 3建模坐标系便于进行几何操作
世界坐标系和建模坐标系之间相互转换:简单的线性变换,如平移、旋转、放缩、剪切以及这些简单变换的组合
多边形表示:
多边形表示物体的主要来源
三维测量与扫描
断层扫描重建
解析数学公式的逼近
参数表示:
参数曲线表示
- 参数表示的优势
- 参数表示是显式的 对每一个参数值,可以直接计算曲面上的对应点 参数表示的物体可以方便地转化为多边形逼近表示
- 曲面上的几何量计算简便(微分几何):法向、曲率、测地线、曲率线等
- 特殊形式的参数表示的外形控制十分直观 Bézier、B-样条、NURBS (Non-Uniform Rational B-Spline, 非均匀有理B-样条)曲线/曲面
参数曲线:
Bézier曲线
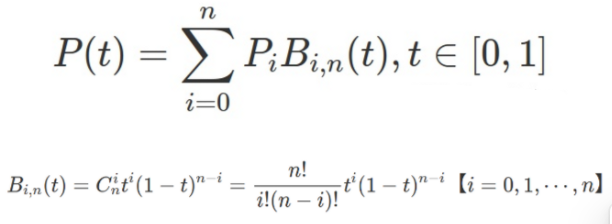

三次 Bézier曲线,由这些点连接形的直线所围成的形状为特征多边形
原理
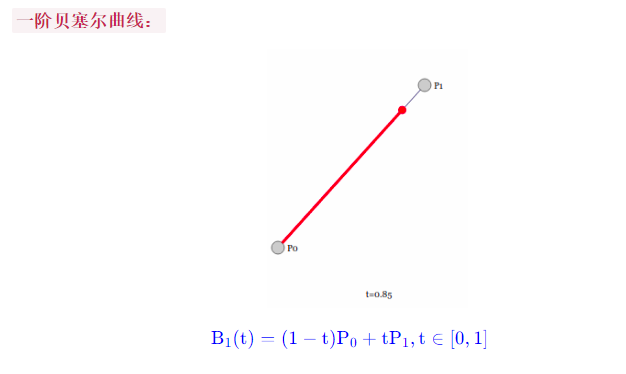
一次贝塞尔曲线很好理解, 就是根据 t来的线性插值
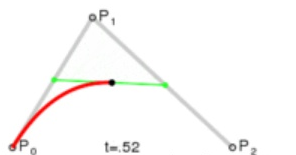
二次贝塞尔曲线

选三个不共线的点ABC,AB上任选一个点P(0)’,BC上点P(1)’使得AP(0)’:AB=BP(1)’:BC

此时P(0)’P(1)’就是视为一次贝塞尔曲线,B1(t)点由一阶贝塞尔曲线的公式得到
当P(0)’和P(1)’随t变动时,就会动态的生成线段P(0)’P(1)’
从而得到二次贝塞尔曲线公式


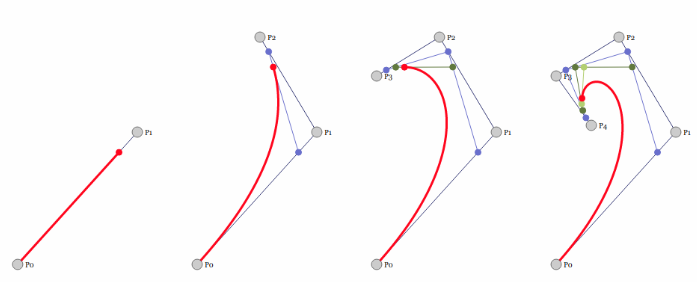
可以想象到n次贝塞尔曲线就会递归调用n-1次的贝塞尔曲线
曲线性质:(点插对几递整凸)
端点插值:第一个控制点和最后一个控制点,恰好是曲线的起始点和终点
**端点切向:**曲线在t=0时的导数是和P0P1的斜率(导数)是相同,t=1时的导数是和P3P4的斜率(导数)是相同
对称性:曲线的控制顶点的几何地位是对称的
递归性:

凸包性:曲线始终会在包含了所有控制点的最小凸多边形中
**几何不变性:**Bézier曲线的形状仅与控制多边形有关,与坐标系无关
整体性质:当移动曲线的一个控制顶点时,整条曲线的形状都会发生改变
表示复杂形状时,需要将多条曲线光滑拼接起来。
B-样条曲线

将多个贝塞尔曲线连接就可以得到B样条
这里有8个控制点,依次用线段连接,B样条曲线由一系列5条3次的贝塞尔曲线连接形成。
一般次数越低(即p越小),那么B样条曲线就更容易逼近他的控制折线
是分段函数,将多个Bézier曲线连接就可以得到B样条曲线
性质
凸包性:曲线始终会在包含了所有控制点的最小凸多边形中
**几何不变性:**Bézier曲线的形状仅与控制多边形有关,与坐标系无关
端点插值:第一个控制点和最后一个控制点,恰好是曲线的起始点和终点
**局部性:**当移动一个控制顶点只影响曲线的一部分不是整条曲线
一般不经过控制点
优点
对于分段Bezier曲线,不同的曲线段相互独立,移动控制点只会影响其所在的Bezier曲线段
B-样条允许局部控制曲线或曲面
缺点
B-样条比Bezier样条更复杂
不能精确表示二次曲面与平面的交线
NURBS曲线
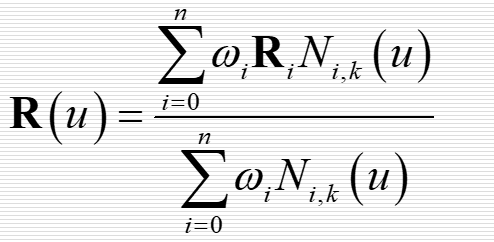
定义
控制点:确定曲线的位置,通常不足曲线上,形成控制多边形
权因子:确定控制点的权值,值越大曲线就越接近控制点
节点矢量u:NURBS曲线随着参数u的变化而变化
特点
非均匀:指节点向量的值与间距可以为任意值。更自由控制曲线形状。
当所有的权因子Wi=1时,就是B-样条曲线,权因子Wi=0时,对应的控制顶点对曲线没有影响,权值越大,越靠近控制点。
- 参数表示的优势
几何表示:
细分曲面
作用
原型设计:主要特点是上手简单且表现力也很丰富(工业设计软件)
在显卡上:游戏场景中
适合于网络传输、用于几何处理、有限元计算(因为面片分布非常的规则、具有计算稳定性)
原理
设计师先勾划出物体的大致轮廓线,然后不断的细化割角。
细分曲面的核心就一个点:细分规则。
常见的细分规则:
1.Catmull-Clark subdivision
是四边形网格的细分法则
- 细分新的曲面,先求出新的曲面的顶点:
Face point(面 → 新顶点(面点))
新的点为:一个面的所有顶点的平均值
Edge point(边 → 新顶点(边点))

- 例子

- 例子
New vertex point(原始点 → 更新点)
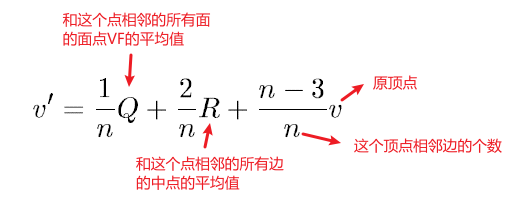
- 细分新的曲面,先求出新的曲面的顶点:
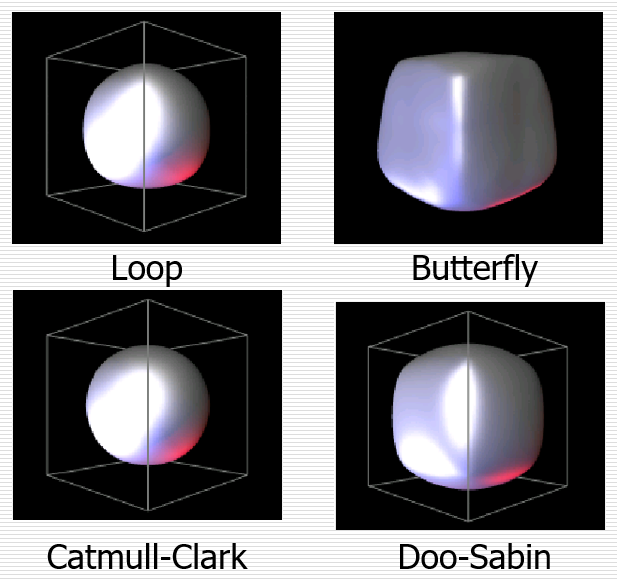
- 循环细分法(Loop细分):以半边数据结构为基础的
- Doo-Sabin细分:二次均匀B样条曲面二分技术的推广
- butterfly subdivision(蝴蝶细分)
细分曲面的翼边储存
Edge 点 面 左边循环 右边循环 Name 起始点 结束点 左边面 右边面 前循环 后循环 前循环 后循环 a X Y 1 2 b d e c
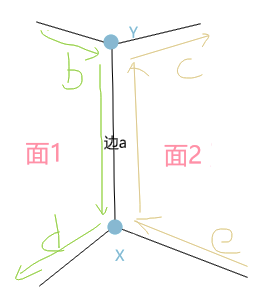
半边数据结构是翼边数据结构的变形,
主要出发点是要改进翼边数据结构,使其在边的数据结构的构造和使用方面更加高效
隐式曲面
物体的CSG树表示
**分解表示:**只关心场景由几个部分组合,不关心由哪些模型构成
# CSG树:
通过一系列几何操作将简单的基本体素组合起来
基本体素:立方体、球、圆柱、圆锥等
布尔运算:并、交、差、补等
几何变换:平移、旋转、放缩、剪切等
如图将模型以树形结构构造成一个复杂形状,可以看出这种方法很复杂,不是不能用来构造一棵树的模型,但工作量大
缺点:1.绘制耗时 2.限制了物体外形的修改 **改进:**混合表示将边界表示和布尔运算结合起来,形成一种界与边界表示和CSG实体表示之间的混合表示
自然景物表示:
分形几何

相似性维数
原图缩小为1/a的相似的b个图形所组成,有:a^D=b,D=logb/loga的关系成立,则指数D称为相似性维数
L-系统
L文法的语法规则:根据语法规则对所给字符进行迭代生成新字符串,每次迭代结果称为一代
字符解释:将字符串中的字符解释为适当的几何体素,就可以得到一个基于语法规则生成的物体
字符集:{A, B, [, ], (, )} 语法规则:A→AA; B→A[B]AA(B) 其中:“A”表示一个主干,“B”表示一个分支,“[ ]”表示分支向左45°,“( )”表示分支向右45°
例子:
B A[B]AA(B) AA[A[B]AA(B)]AAAA(A[B]AA(B))



