 渲染通道、三维变换
渲染通道、三维变换
# 渲染通道、三维变换
Owner: -QVQ-
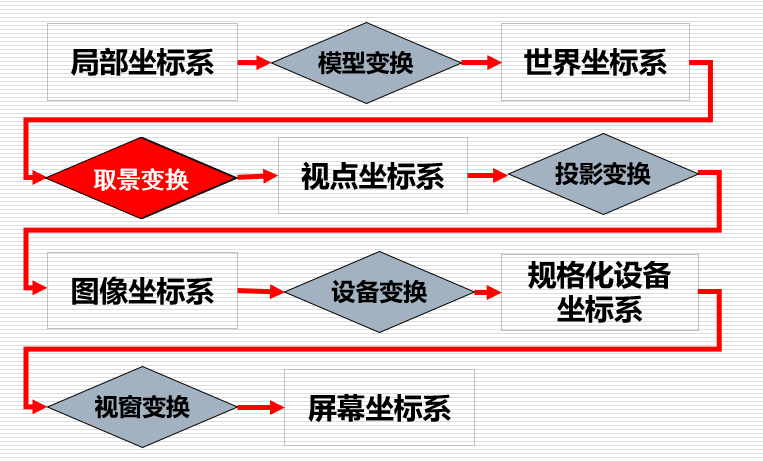
三维变换流程图
照相机模型
模型:
小孔成像模型(通用):
所有捕捉到的光线都沿着指向焦点的路径到达,没有镜头变形(所有物体都处于焦点位置) 传感器响应与射线成比例
其他模型包括: Depth of field Motion blur Lens distortion
外参
相机的位置、朝向:
求外参矩阵:把XwyW,Zw转换为以相机为中心的世界中的坐标xc,yC,zc
小孔成像问题:
将转换为相机为中心世界的Xc,yC,ZC,利用相机内参转换为图片中的点的位置,在将 图片中的点转换为是哪个像素(像素坐标)
内参
光圈、视平面
变换pipeline
已知变换:平移,旋转,缩放,他们被用于三个作用:
渲染通道:
模型变换
大小缩放,平移,旋转物体 建模坐标系->世界坐标系
光照计算
光源发散、表面反射、大气衰减、相机感应
间接光照、全局光照
视窗变换
剪裁
投影变换
透视投影,平行投影
光栅化
转换图像坐标系为像素和颜色,这里也可以处理消隐

走样
二维变换
基本变换:平移、旋转、放缩 其它变换:剪切、对称、复合
齐次坐标
用n+1维向量表示一个n维向量
◆二维点(x, y),用(X, Y, Z)表示(X=X/Z, Y=Y/Z) (2,3)的齐次坐标表示可以是(4,6,2)、(3,4.5,1.5)
优势:防止浮点数溢出、矩阵变换的统一表示
二维平移
二维点P(x, y)移动(tx,ty)后,得到点P'(x', y')

将矩阵的加法转变为矩阵的乘法
二维旋转
将点P(x,y)绕坐标原点按逆时针旋转角


二维缩放

剪切变换
变换过程中,坐标保持不变,x坐标值发生线性变化 平行于X轴的线段变换后仍平行于X轴,平行于Y轴的线段变换后错切成与Y轴成固定角α的直线

对称变换




复合二维变换
平移、旋转和放缩矩阵通常记为T、R和S,TSA表示对A先T变换再S变换 二维变换具有结合性:(AB)C=A(BC) 二维变换不具有交换性A8 C
刚体变换: 可以分解为:平移和旋转的组合 物体的形状没变化,位置和方位有变化
仿射变换: 可以分解为:平移、旋转和放缩的组合 保持点的共线性、长度的比例=>平行线
三维变换
是:三维变换可以看作是对照相过程的模拟,即如何将场景中的三维几何物体变换到二维屏幕上
变换内容包括:世界坐标系和造型变换、视点坐标系和取景变换、投影坐标系和投影变换、屏幕坐标系和设备变换(27英寸到32英寸)

坐标系:视点坐标系(虚拟照相机的位置、朝向以及向上的方向) 变换:取景变换(在视域四棱锥进行裁剪和背面剔除)

三维变换流程图
平移

缩放

旋转(与二维不同)
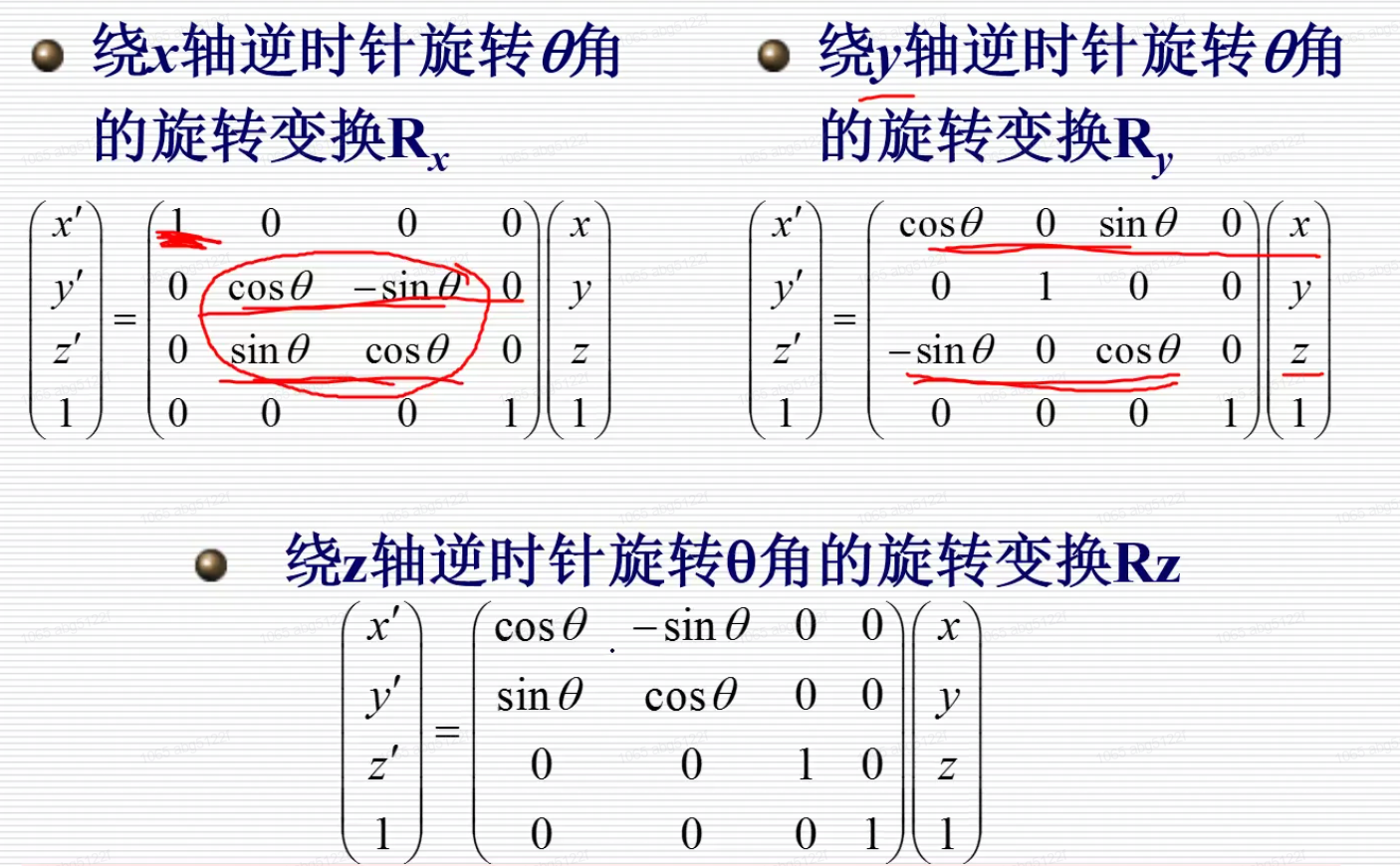
非线性变换(扭曲)

视点坐标系和取景变换
视点坐标系定义于世界坐标系中 定义了照相机镜头的朝向:视线方向 照相机的位置 UP方向
投影变换
投影点:通常取视点坐标系中(0,0,0)点 投影平面:取作与视线方向N方向)垂直的平面n坐标=d。假设在视点坐标系中的点为(u,y,n), 那么在投影面上的对应点坐标(u,')为


一维透视
二维:投影加上一个变换矩阵,即做一次旋转
三维:先使立体绕Z轴旋转一个角度,再绕X轴旋转个角度中(类似于轴测变换),这样使得立体上原平行于三个坐标平面的表面均与投影面XOZ产生一定的倾斜角;向XOZ投影面作透视投影。

视域四棱锥裁剪

平行投影的视域四棱锥一般为长方体
视野范围在视域四棱内、“前面”“后面”之间的部分四棱锥
规格化设备坐标和设备变换
在投影平面上,有一个矩形区域称为视窗
“视域四棱锥” 图中的矩形 物体投影后:二维齐次坐标表示
设备变换:投影后二维齐次坐标除以最后一个坐标分量,便得到了规格化设备坐标
屏幕坐标系和视窗变换
屏幕坐标系:通常以像素为单位 视窗变换
二维变换:将定义在视窗中的规格化设备坐标转换到以像素为单位的屏幕坐标 扫描转换:将连续的几何物体转换为离散的光栅表示


