多边形

Owner: -QVQ-

• 多边形表示物体的主要来源

  三维测量与扫描

  断层扫描重建

  解析数学公式的逼近

• 多边形表示方法

  • OBJ格式（3D模型文件）

    组成：

    1. 顶点坐标表(x, y, z) ：每个顶点处可能有多个平面片，一般情况下顶点数小于面片数。

    2. 纹理坐标表(u, v)：控制纹理映射时纹理在表面上的位置。

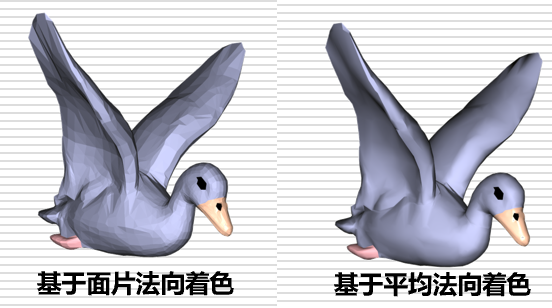
    3. 法向表 (nx, ny, nz) ：控制物体绘制时的着色光滑程度 如果顶点法向为取作该面片的法向，绘制出来的多边形物体棱角分明 如果顶点法向是周围面片法向的某种平均，则绘制结果是光滑的

    4. 面表：由指向顶点、纹理坐标以及法向的指针组成。

    特性：

    (1)3D模型文件，因此不包含动画、材质特性、贴图路径、动力学、粒子等信息。

    (2)主要是多边形模型。虽然OBJ文件也支持曲线(Curves)、表面(Surfaces)、点组材质(Point Group Materials)，但Maya导出的OBJ文件并不包括这些信息。

    (3)OBJ文件支持三个点以上的面。（如果只支持三个点的面，导入模型会被三角化）

    (4)OBJ文件支持法线和贴图坐标。贴图坐标信息可以存入OBJ文件中。

• 三角形网格表示的数据结构

  边界表示（BRep表示），它是几何造型中最成熟、无二义的表示法。

  如下：

  其中

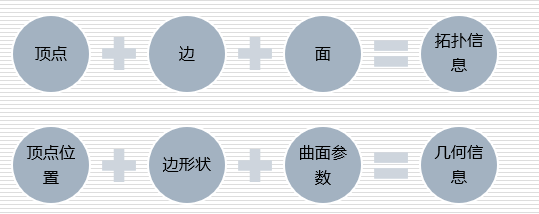
  拓扑信息是指：

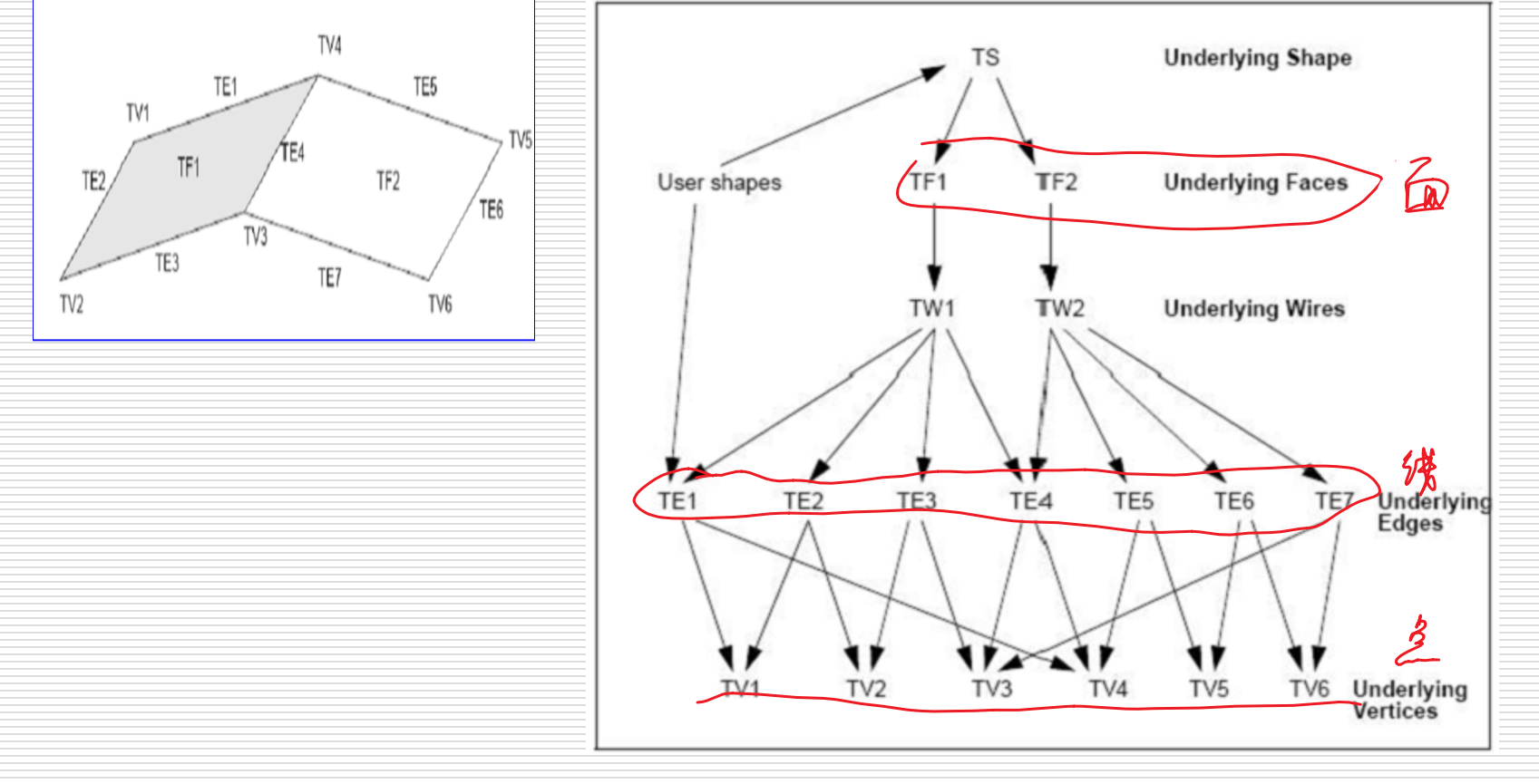
  点线面的拓扑结构

  • 半边表示的数据结构包括：

    • 半边结构(Half-Edge Structure)：可定向的二维流形及其子集

      表示方法略微复杂的边

      大多操作都可以在常数时间完成。

      数据结构的大小是固定的（没有使用动态数组）且紧凑的。

      • 数据结构(每条边被记为两条半边，记录每条半边)

        边：

        起始顶点的指针

        邻接面的指针(如果为边界，指针为NULL )

        下一条半边(逆时针方向)

        相邻的半边

        前一条半边(可选)

        面：

        边界上的任意一条半边 顶点：

        xyz的坐标值

        此顶点为起点的所有半边

        struct HE_edge
        {
        	HE_vert* vert; // 起始顶点的指针
        	HE_edge* pair; // 相邻的半边 
        	HE_face* face; // 邻接面的指针
        	HE_edge* next; // 下一条半边
        };
        

        一个例子:

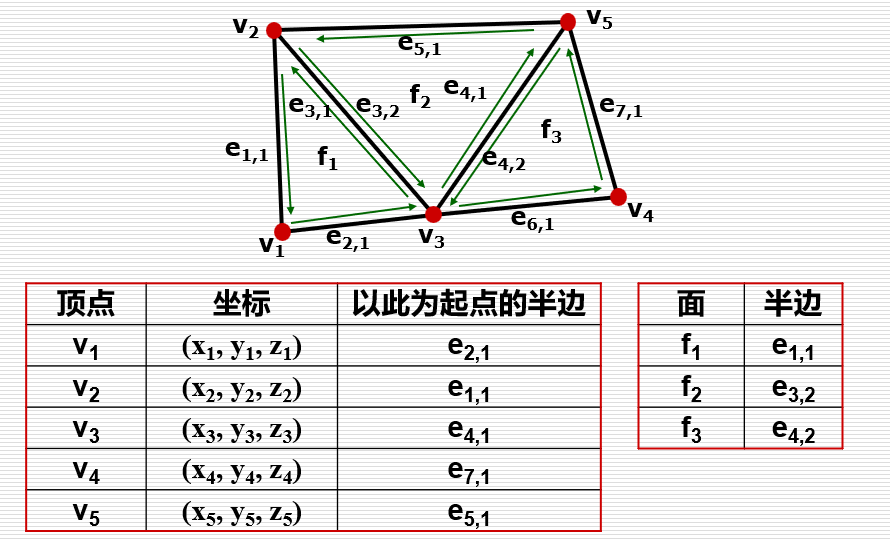
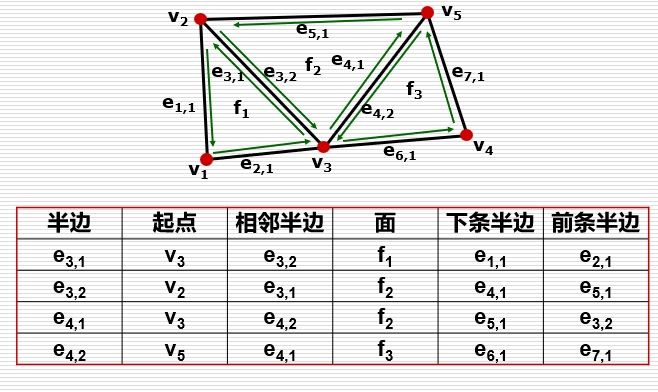
        面存放了边，边存放了点

      优势：

      查询时间 O(1)， 操作时间 (通常) O(1) 缺点：

      只能表示可定向流形（T-型接合、内部多边形、网格中的空缺，不能使用）

      信息冗余

    翼边数据结构

    辐射边数据结构

  • 多边形表示的优点

    表示简单 可以表示具有任意拓扑的物体 可以表示具有丰富细节的物体 大部分图形硬件支持多边形物体的加速绘制

  • 多边形表示的缺点

    逼近表示，难以满足交互时放大要求 难以用传统方法修改(编辑)物体外形 缺乏解析表达式，几何属性计算困难 在表示复杂拓扑和具有丰富细节的物体时，数据量庞大，建模、编辑、绘制、存储的负担重