变换

Owner: -QVQ-

• 齐次坐标（投影坐标）

  作用：用于投影几何里的坐标系统，可让包括无穷远点的点坐标以有限坐标表示，进行仿射变换，通常其投影变换能简单地使用矩阵来表示。

  与笛卡尔坐标相比：齐次坐标公式表示通常更简单且对称，

  定义：

  在齐次坐标里，需要两个值来表示在投影线上的一点，需要三个值来表示投影平面上的一点

  例：( X , Y ) (X, Y)(X,Y) 在齐次坐标里面变成了 ( x , y , w ) ，并且有 X = x / w , Y = y / w (1，2) 的齐次坐标可以表示为 ( 1 , 2 , 1 ) ，如果点 ( 1 , 2 ) (1, 2)(1,2) 移动到无限远处，

  然后它的齐次坐标表示为 ( 1 , 2 , 0 ) (1, 2, 0)(1,2,0) ，因为 ( 1/0 , 2/0 ) = ( ∞ , ∞ )

• 变换矩阵（记住坐标变换矩阵）

  刚体变换：形状没变化，位置和方位改变

  平移T

  绕原点逆时针旋转R

  笛卡尔坐标

  （非线性变换）

  笛卡尔坐标

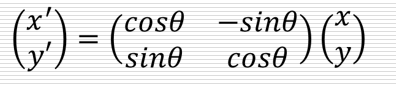
  （线性变换）

  齐次坐标变换

  齐次坐标变换

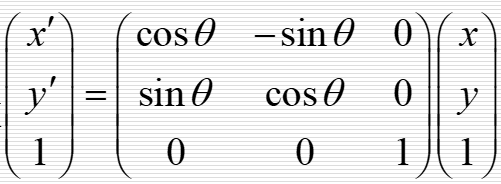
  • 上诉是变换矩阵在坐标点的左侧，如果变换矩阵在坐标点的右侧

    例：将下面的多边形围绕点P逆时针旋转90

    以下两个方法一样：

    1. X1为新的坐标点，X为旧的x,y,z坐标

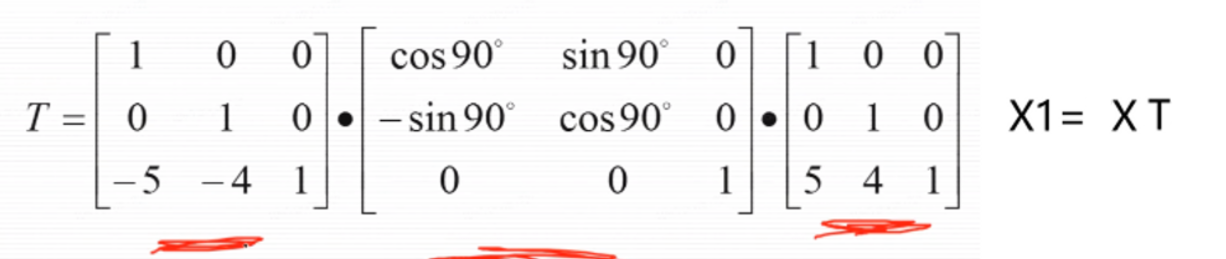
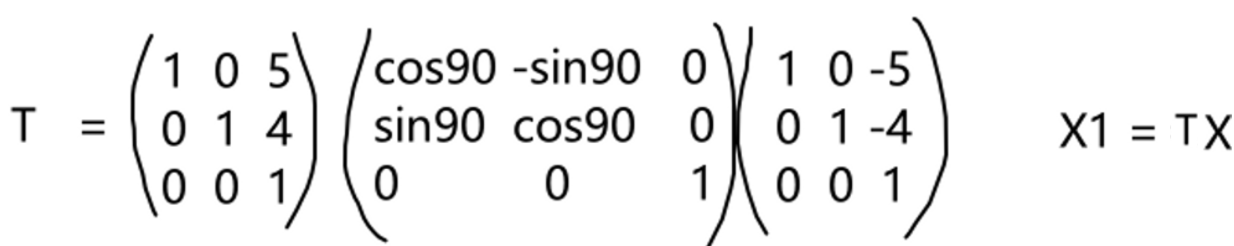
- 证明

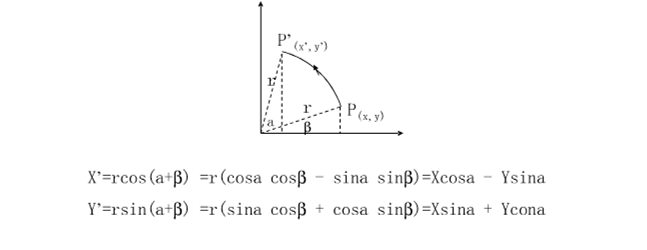
**仿射变换：**

**放缩S**

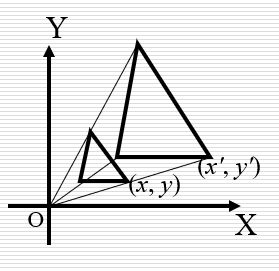
笛卡尔坐标

（线性变换）sx和sy为x和y分量的放缩比例

齐次坐标

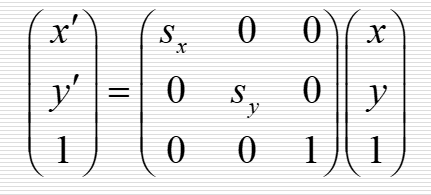
二维变换具有结合性：(AB)C=A(BC)、不具有交换性

线性变换：笛卡尔坐标中可以通过一个矩阵实现

非线性变换：笛卡尔坐标中不可以通过一个矩阵实现

变换流程：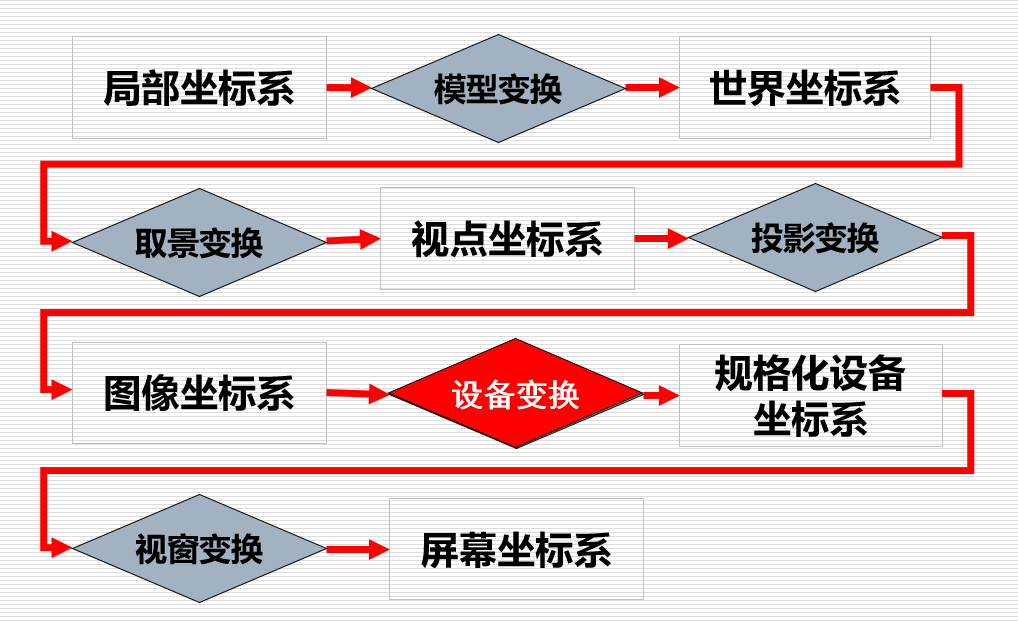

三维变换流程图

• 模型变换（在场景坐标系下）

  物体从建模坐标系到世界坐标系的变换（包括三维线性和非线性变换）

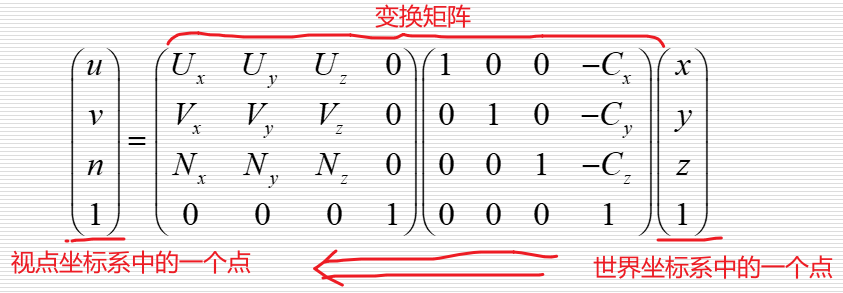
• 取景变换（生成视点坐标系）

  视点坐标系定义于世界坐标系中

  需要确定：

  1. 相机的位置C：坐标原点C=(Cx, Cy, Cz)

  2. 镜头的朝向N：单位向量N=(Nx, Ny, Nz)

  3. 计算V：（计算后单位化）（代表镜头朝向与UP向量的夹角）

     UP：与镜头朝向不平行的向量

  4. 计算U：（计算后单位化）

  以上四个矢量C、U、V、N组成视点坐标系，从而得到世界坐标系到视点坐标系的变换

• 投影变换（在视点坐标系中，将三维场景变为二维图像（二维齐次坐标），生成图像坐标系）

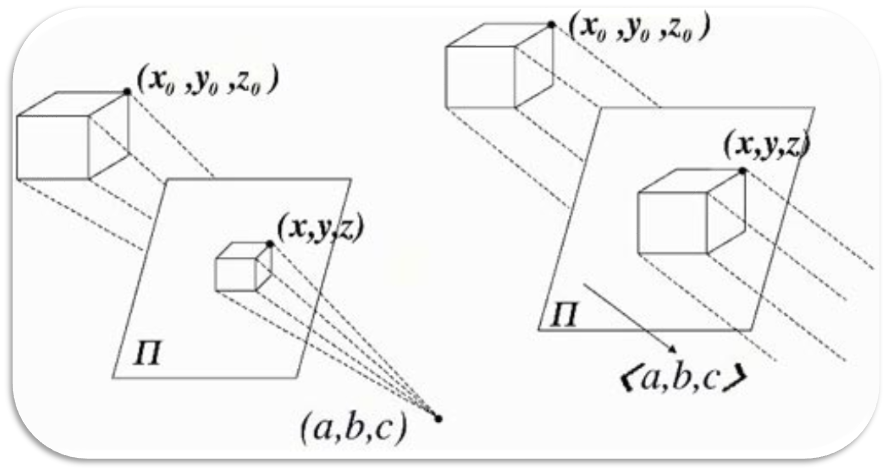
  • 透视投影：符合人类的视觉特点，产生的投影效果更为真实

    投影点：通常取视点坐标系中(0, 0, 0)点 投影平面：取作与视线方向(N方向)垂直的平面n = d。假设在视点坐标系中的点为(u, v, n)，那么在投影面上的对应点坐标(up, vp)为

  平行投影：物体的相对度量保持不变，适用于建筑和机械设计

  • 剪裁

    位于视域四棱锥内部的几何物体被投影在投影平面上，位于外部剔除。部分位于内部，需裁剪

• 设备变换（生成规格化坐标系）

  投影后二维齐次坐标除以最后一个坐标分量W，便得到了规格化设备坐标

• 视窗变换（生成屏幕坐标系）

  屏幕坐标系：通常以像素为单位 视窗变换： 二维变换：将定义在视窗中的规格化设备坐标转换到以像素为单位的屏幕坐标 **扫描转换：**将连续的几何物体转换为离散的光栅表示