 特征点提取
特征点提取
# 特征点提取
Owner: -QVQ-
目的:为了能实现视图之间的通信,通过图像能匹配点,块,边,区域

特征点的用途:
- 图像对齐
- 3D重建
- 运动跟踪
- 机器人导航
- 图像检索
- 目标识别
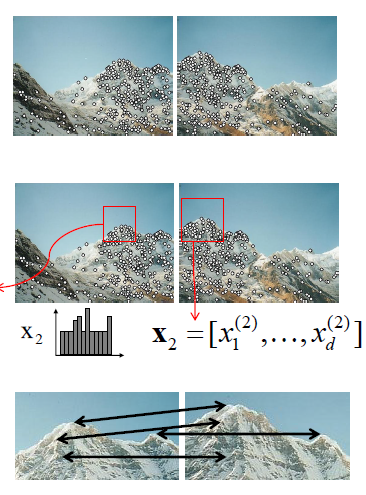
# 有两张图片如何合成一张图片

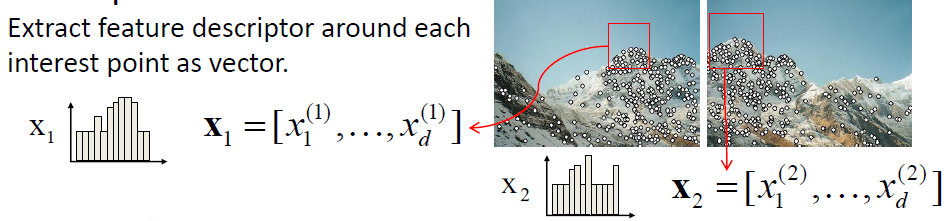
局部特征点的提取过程:
检测
找特征点集
描述
提取每个特征点周围的特征信息组成矩阵
匹配
计算两个特征矩阵的距离去寻找符合的
# 什么是好的特征点
- 可重复性:尽管进行了几何和光度变换,但在一些图像中可以发现相同的特征
- 独特的:每个特征都是独特的
- 紧凑和高效:比图像像素少得多的特征
- 位置特征:占据图像中相对较小的区域,抗杂波和遮挡
# 角点检测
角点
图像梯度在两个或多个方向上有变化,角点要有足够的可重复性和显著性,一定不会出现在直线上。
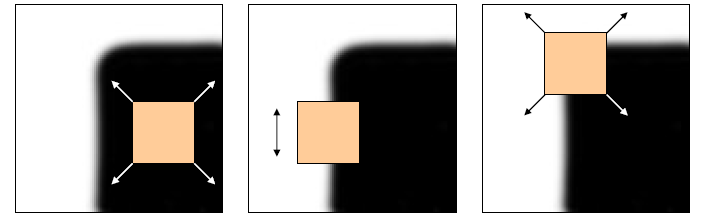
平面:在各个方向都没有变换
边:在边上没有变换
角点:在所有方向都有较大变换
基本思想:我们不确定这个图像的特征点将匹配其他哪些图像,但我们能计算一个位置相对于位置u的微小变化在外观上有多稳定。
移动[u,v]时,窗口函数w(x,y),强度I(x,y),得到角点E(u,v)
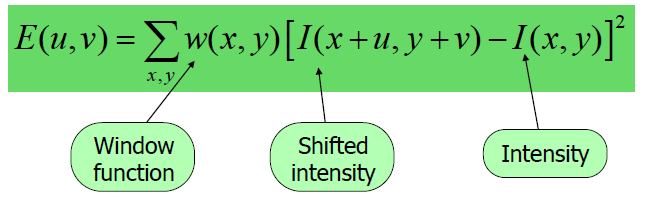


如果对每一个点执行这样的操作,开销很大
我们想得到E对于小变换的行为,我们知道E在高峰的行为,我们能用 二次曲面去近似E(u,v)
将E(u,v)泰勒展开
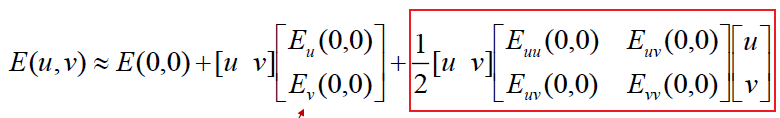
忽略E(0,0)和一次部分,仅看二次部分
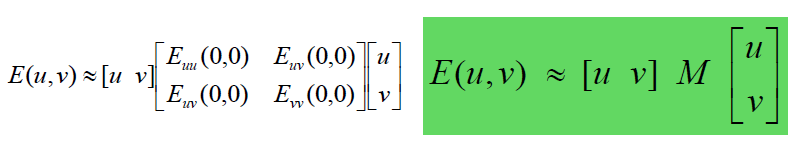
而M可以化简
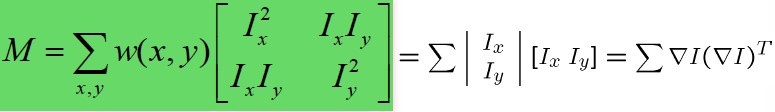
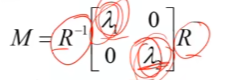
这里的λ1、λ2代表x、y方向的强度
从左图到右图为二次矩阵的可视化

Harris角点探测器:
0.输入图像

# 1.计算图像的导数(再之前可以选择是否先用平滑过滤器)
# 2.用二阶导数计算M部分
# 3.使用高斯滤波器
# 4.计算角点
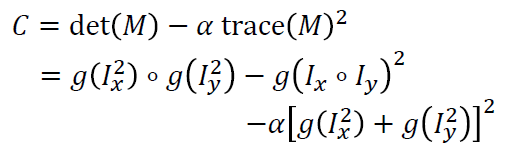
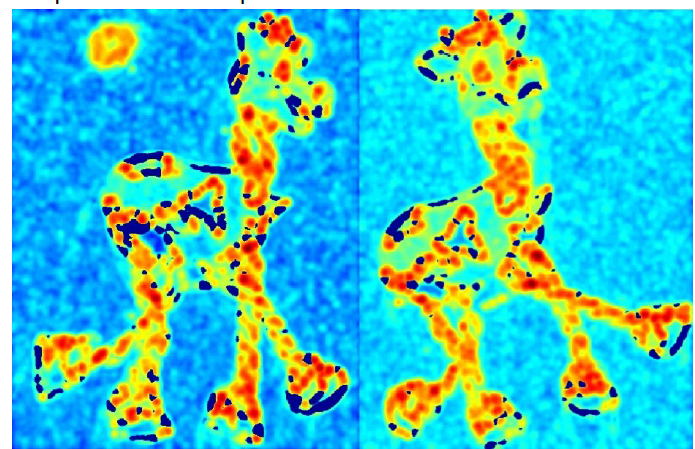
# 5.非最大抑制,找到具有较大角点响应的像素点(C>阔值)
# 6.找到局部最大像素点

# 尺度选择特性SIFT-拉普拉斯
对于角点平移和旋转不改变。
光照亮度也不部分不改变,部分 体现在提高亮度后一些看不见的值出现了
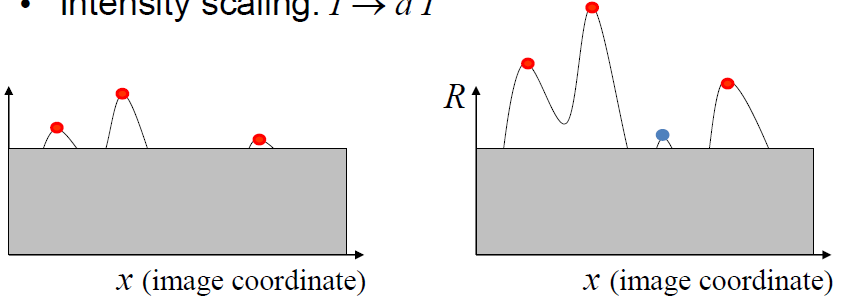
但缩放会改变,角点放大后会被分类成边缘
当前的任务是找到一个f()对等比例缩放依然能 正确匹配
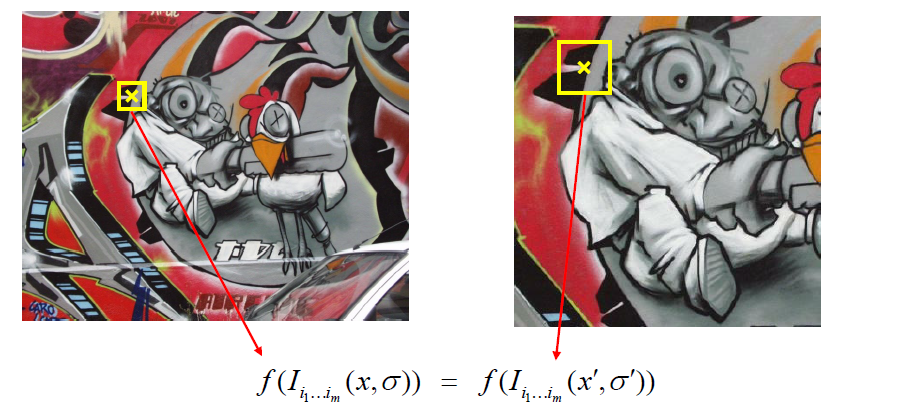
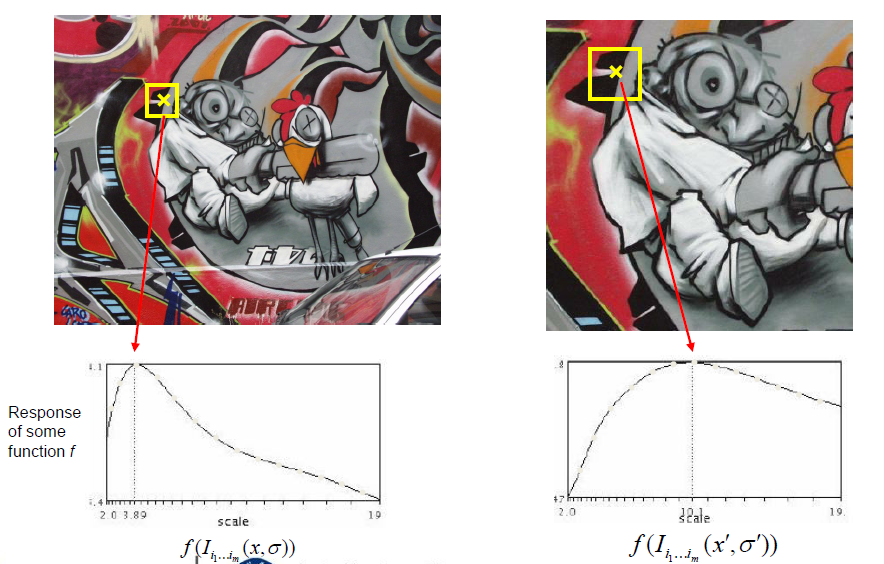
Blob检测器是角点检测常用的,他是高斯二阶导,又叫拉普拉斯算子,其中可变参数只有б方差
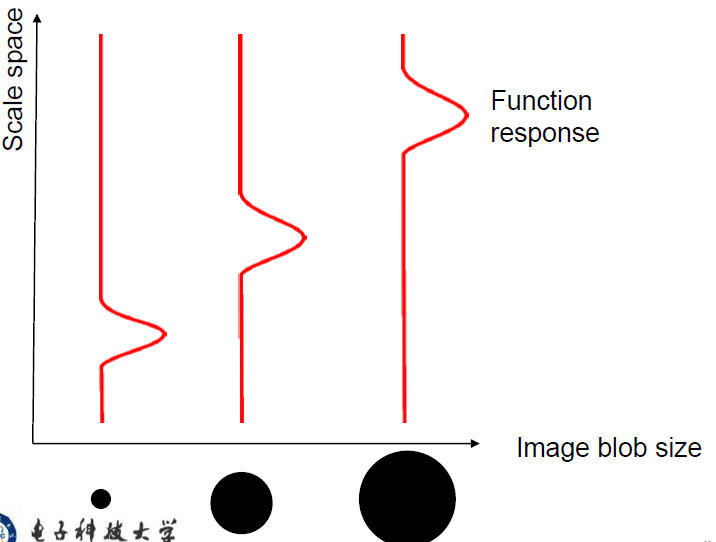
当信号和二阶导匹配时一定能产生一个最大值 ,即尺度匹配
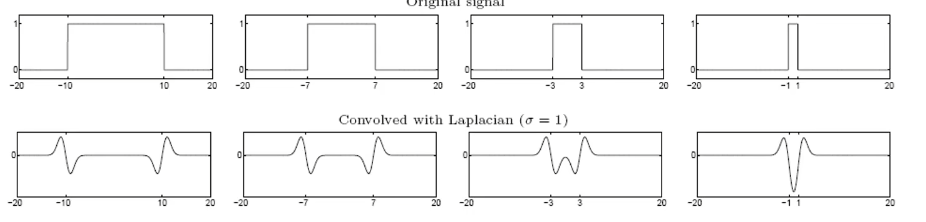
此时变信号,模板不变,可以找到和模板对齐的信号,但实际上事先不知道信号
所以预先用多个模板进行匹配,但随着б方差的变大,模板变平,直至没有信号
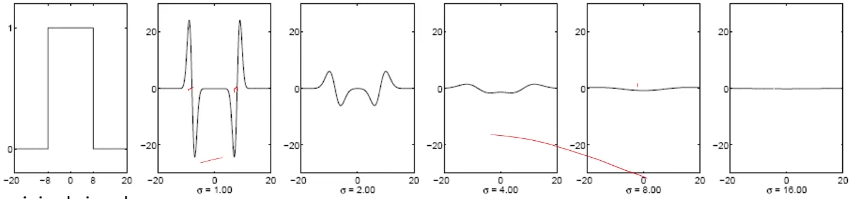
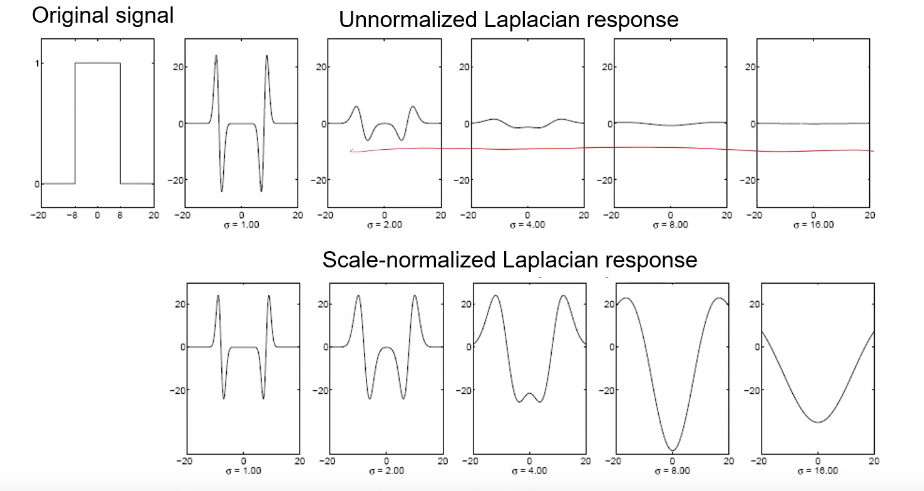
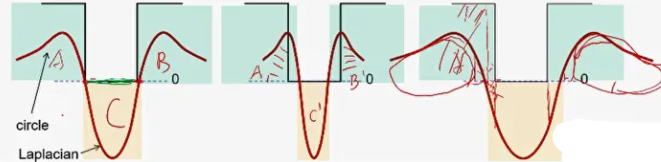
假如现有如图中红色线所示的信号,使用蓝色(高斯一阶偏导)的卷积核进行卷积,其中上半粉色区域的面积如图,显然随着б的增大,这个面积会越来越小,最终肯定是趋于0了呀。那么如果对其处理一下呢,自然就想到对这个响应值再乘一个б,对于拉普拉斯就是再乘б2

对比补偿前后:这样就能完成尺度的自动检测。这样就完成了一个多尺度的检测。
下图黑色为图像信号,低频处代表没有颜色,红色为拉普拉斯图像,在作卷积运算时,即黑色的值乘以红色的值,只有图一完美匹配时得到的是最大值,图二红色信号有一部分对应的图像信号为0,图三有图像信号的部分对应的拉普拉斯信号有一部分为负数。
基于这个理论,在进行匹配时,我们只需保留当前位置的最大值,具体做法是在相邻的两个方差生成的模板图内的9个像素和自己相邻的8个像素共26个像素点处的卷积值的最大值保留下来
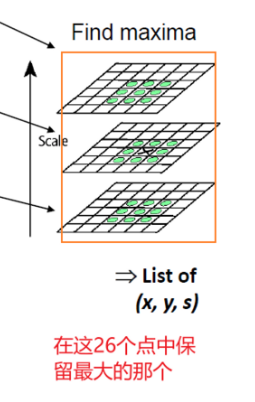
并以这些点为圆心作圆,б越大,圆半径越大,这些圆代表了规模,每个圆代表具有最大尺度响应的描述符,

梳理上面的流程,图像的每个点都和不同б的拉普拉斯图作卷积运算,保留最大的尺度
对每一个点都做卷积耗时太大,可以选择只对角点处做卷积,这是一个有效的实施特征点匹配的方法(Harris+拉普拉斯)
# DOG(高斯差分)
前置知识:高斯金字塔
分为很多组,第一组第一层为初始,用б作平滑得到第二层,kб平滑第二次得到第三层,以此类推。第二组一定从第一组的倒数第三层开始,作比例因子为2的降采样得到第二组第一层,然后和对第一组一样继续作平滑。
同组内尺寸一样,只是平滑因子不同,不同组,第2组是第1组图像的一半,O组L层就构成了高斯金字塔

# 第一步:生成DOG金字塔
通过对两个相邻高斯尺度空间的图像相减,得到DOG的响应值图像

先用б的卷积核对原图卷积,再用DOG的响应值图像,依次卷积,即不用分别计算б、kб、2kб的图像,而是在б的图像上通过DOG计算Kб卷积后的图像,再在这个图像上通过DOG计算2Kб的图像
意义:高斯卷积核的宽度通常选择3倍的方差,而用DOG通常会小一些
K取【1,2】
# 第二步:空间极值点检测
同组内相邻的两个方差生成的模板图内的9个像素和自己相邻的8个像素共26个像素点处的卷积值的最大值保留下来
对于DOG金字塔每组的最上和最下面的那层,用高斯模糊多模糊出高斯金字塔的3层来凑数(3层的DOG金字塔需要多两层,对应5层的高斯金字塔需要多两层,即高斯金字塔要多三层才行)
即如果要输出的尺度为S=3,就需要计算6层高斯响应
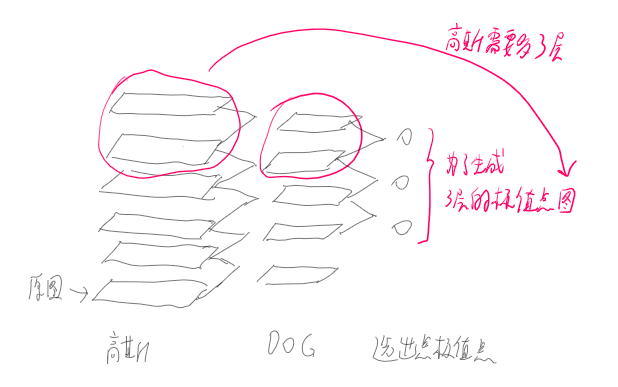
比如要检测10个尺度,DOG有12层,高斯有13层
# 第三步:稳定关键点的精确定位
DOG值对噪声和边缘比较敏感,所以在第2步的尺度空间中检测到的局部极值点还要经过进一步的筛选,去除不稳定和错误检测出的极值点。
利用阔值的方法,即非最大抑制
# 第四步:稳定关键点的方向信息匹配
计算检测点周围16*16窗口的方向,统计每个方向出现的次数,可以做如下设定:直方图的峰值为主方向的参数,其他高于主方向百分之80的方向被判定为辅助方向。
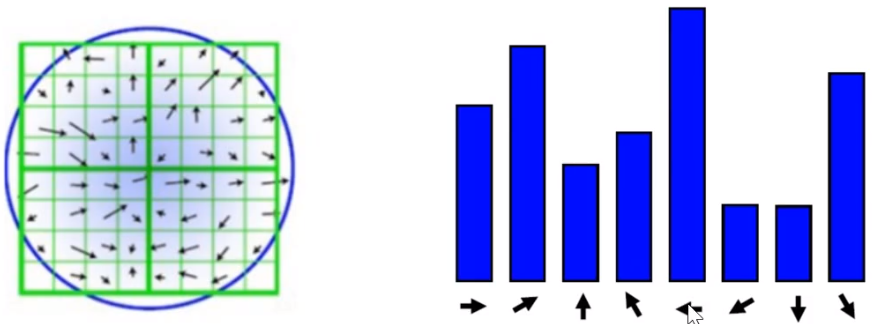

这样做能够得到 纹理、方向信息、SIFT尺度不变特性转换
# 第五步:关键点描述
第四步得到16*16的关键点方向信息图,这一步精简信息量得到关键点描述子
对关键点周围像素分块,计算块内梯度直方图,即向量,每个向量只取前8个辅助方向,图中显示分块为22,但实际上分块是44,即每个关键点对应16个向量,则有448=128个维度。
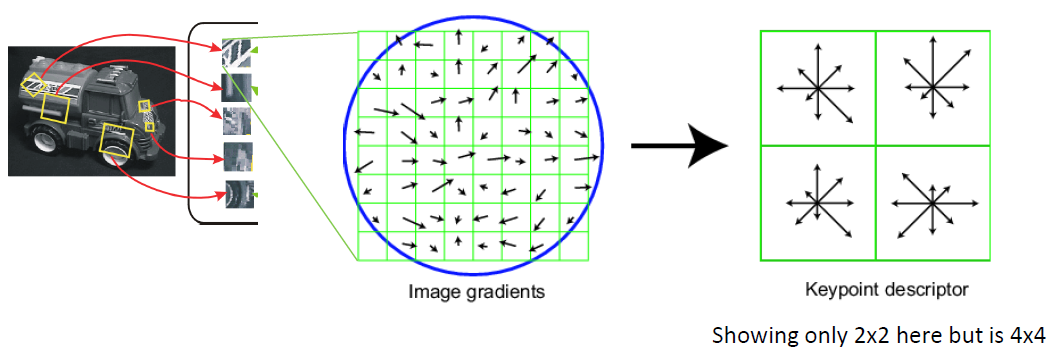
通过上诉方式为每个关键点建立一个描述符,用一组向量将这个关键点描述出来,使其不随各种平移缩放旋转变换而改变。描述子不但包含关键点,也包含关键点周围对其有贡献的邻域点
# 特征点匹配
一到三步在做特征点的检测,四到五步是找到描述信息
就是对模板图和实时图分别做上面五个步骤建立关键点描述子集合,做匹配可以用穷举法
欧式距离:
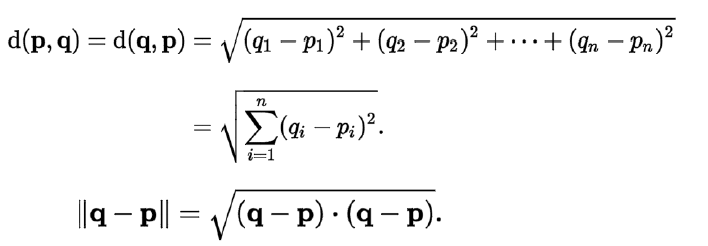
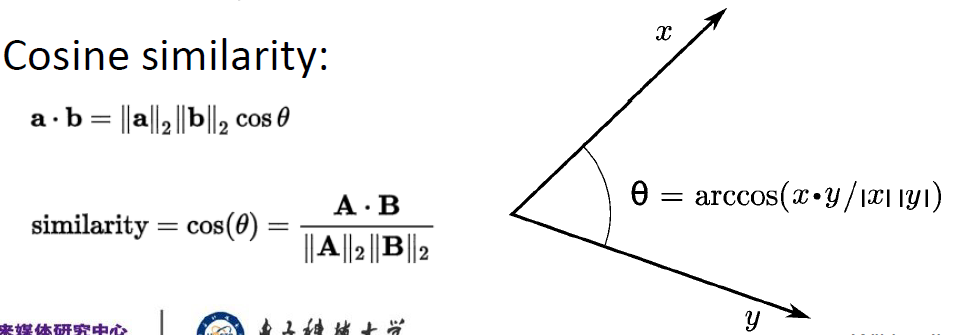
余弦相似度:
# 方法一:暴力匹配(最小距离法)
- 计算特征空间中的欧式距离,例如128个模糊SIFT描述符之间的欧氏距离
- 取到匹配点的最小距离(最近的邻居)
# 方法二:暴力匹配(距离阈值法)
- 计算特征空间中的欧式距离,例如128个模糊SIFT描述符之间的欧氏距离
- 取到匹配点的最小距离(最近的邻居)
- 忽略任何高于阈值的
即待匹配目标与模型之间的距离小于某个阈值,则认为匹配上了,
方法非常简单,但是阈值的确定非常困难,
问题:阈值很难选择,另外非显著特征可能有很多紧密匹配,只有一个是正确的
# 方法三:最近邻近距离比率(NNDR)
比较最近邻(NN1)和次近邻(NN2)特征向量的距离
如果相似,则比率NN1/NN2≈1
如果NN1小,则比率趋于0
按这个比率排序,将匹配按置信度排序。
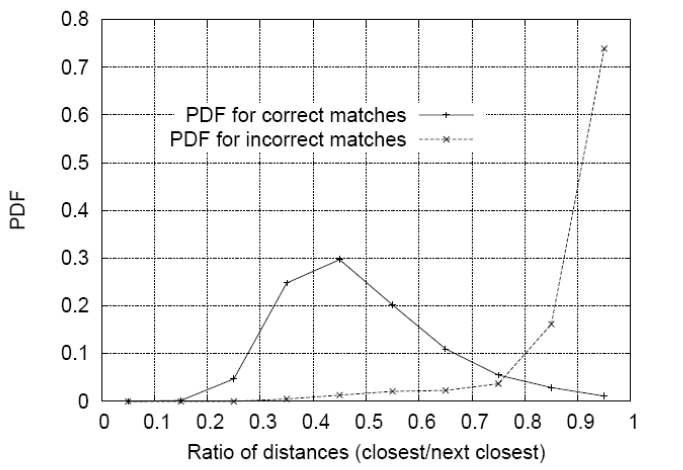
比率阈值取决于应用程序对假阳性和真阳性数量之间权衡的看法!
features_imagel * features_image2T
# 方法四:交叉匹配
进行一次匹配,反过来使用被匹配到的点进行匹配,如果匹配到的仍然是第一次匹配的点的话,就认为这是一个正确的匹配


