 滤波器(卷积核)
滤波器(卷积核)
# 滤波器(卷积核)
Owner: -QVQ-
# 定义
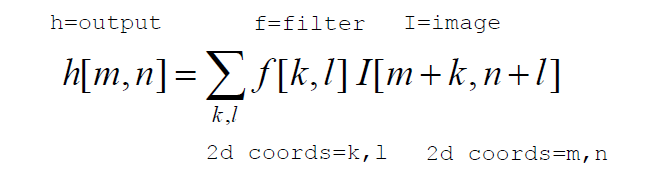
# 功能
整体上说
spatial domain (空域)
图像数字矩阵的算术操作,例如:平滑、锐化
frequency domain (频域)
修改图像的频域,例如:降噪、采用、压缩
Image pyramids (图像金字塔)
图像金字塔是什么
以多分辨率 (opens new window)来解释图像的结构,是自下而上分辨率逐步降低,且来源于同一张原始图的图像集合。其通过梯次向下采样获得,直到达到某个终止条件才停止采样得到。
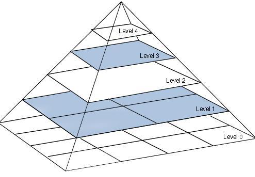
实现图像金字塔向下拓展,即从低分辨率生成高分辨率的图像
具体而言:
- 图像增强:变形、去噪、增加对比度
- 提取信息:纹理、边缘、特征点
- 图像识别
# 常见的滤波器(卷积核)
# box filter平滑滤波器
它用邻近的像素点的平均值代替当前像素点的值,实现了平滑的效果
下面左图通过box filter计算后为右图

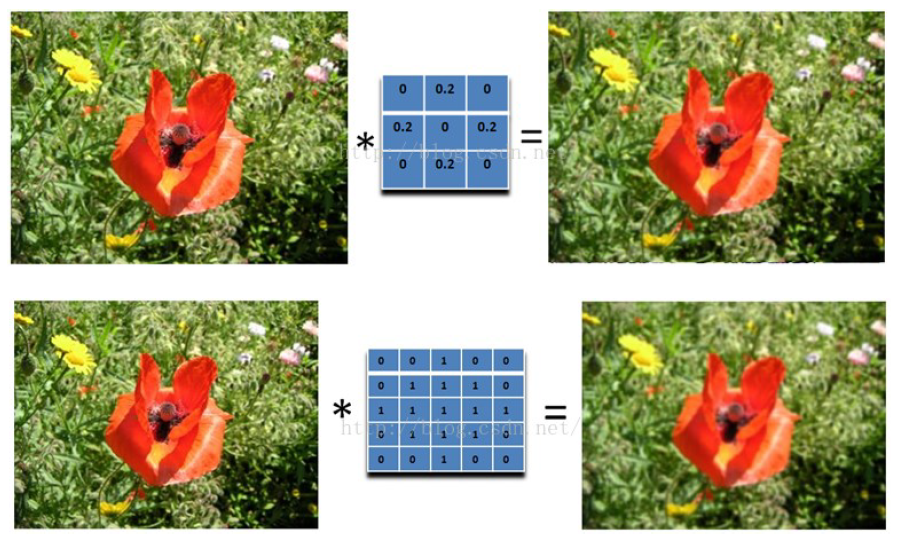
# 单位脉冲核
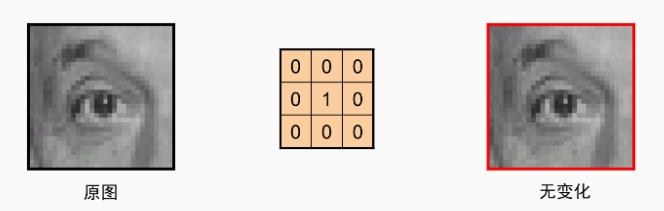
# linear filters
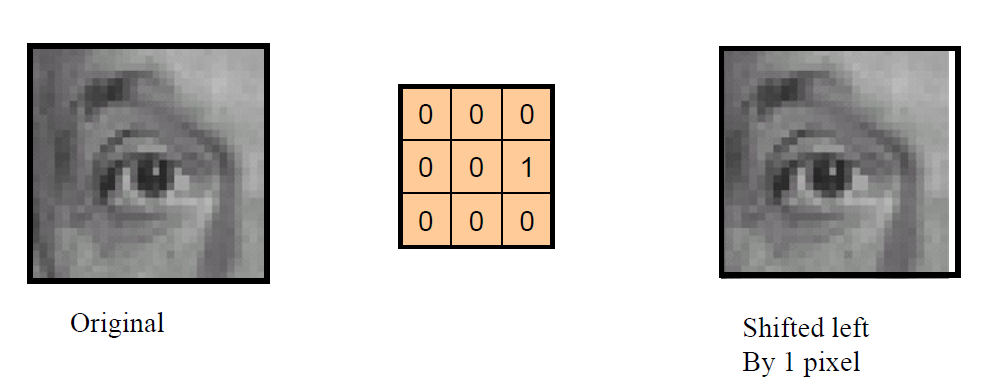

保留并加强了垂直方向的线条,舍弃了方向模糊的点

保留并加强了水平方向的线条,舍弃了方向模糊的点
# 锐化滤波器Sharpening fileter
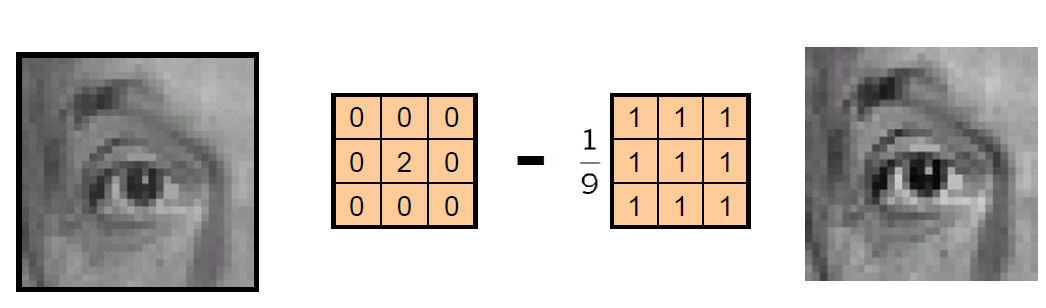
加强了点与周围平均值的差异
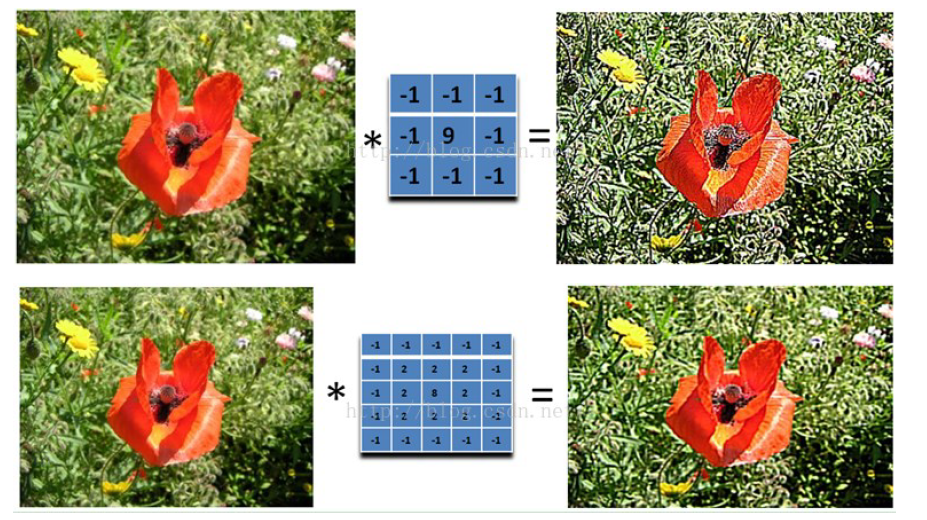
锐化滤波器所有元素之和是1
# Edge detection Filter边缘检测滤波器

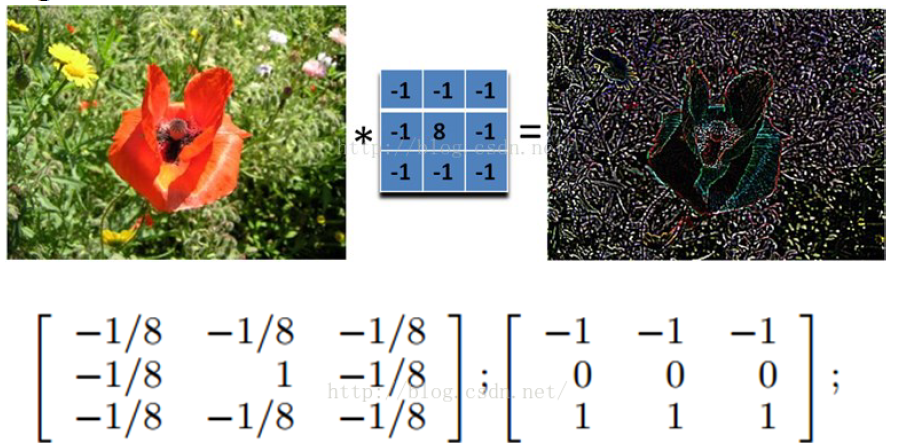
边缘提取滤波器所有元素之和是0
# Embossing Fileter


滤波器是不对称的,有方向的
# Motion Blur Filter动态模糊滤波器

滤波器是有方向的
对称滤波器通常用于平滑和模糊处理,而反对称滤波器通常用于边缘检测和锐化处理。
# 高斯模糊滤波器
下面提及
# 滤波器的一些规范
•滤波器的大小应该是奇数,这样它才有一个中心,例如3x3,5x5或者7x7。5x5大小的核的半径就是2。
•滤波器矩阵所有的元素之和等于1,则图像的亮度保持不变
•滤波器矩阵所有的元素之和大于1,更亮,小于1,变暗。和为0,图像不会变黑
•对于滤波后的结构,可能会出现负数或者大于255的数值。对这种情况,我们将他们直接截断到0和255之间即可。对于负数,也可以取绝对值。
# 卷积和协相关Convolution and Correlation
这代表了图像和卷积核或者滤波器作交互的操作方式
2d Correlation
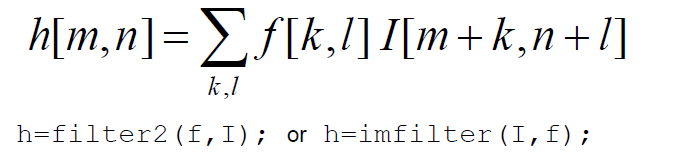
2d Convolution
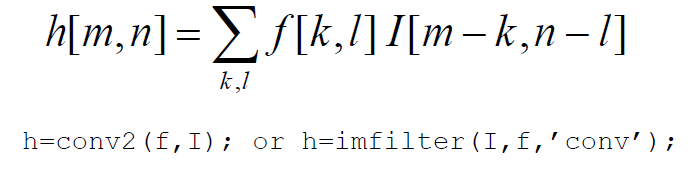
卷积,即在对图像进行卷积操作时要对滤波器先水平翻转,再进行竖直翻转
两者都要具有线性和平移不变形的特性:即对两张图先求和再卷积和先卷积再求和结果是一样的
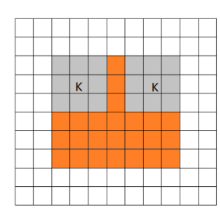
# 卷积的三种模式
full 从filter和image刚相交开始做卷积,白色部分为填0。
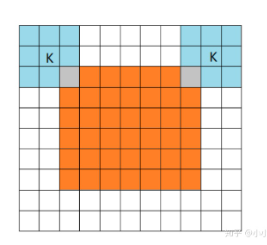
same 当filter的中心(K)与image的边角重合时,开始做卷积运算,可以保证输入输出图尺寸一样(步长为1)
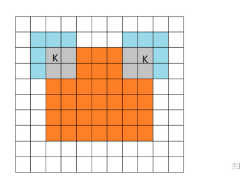
valid 当filter全部在image里面的时候,进行卷积运算
# 噪声的分类
- 椒盐噪声:就是黑点,白点。处理方式:中值滤波
- 脉冲噪声,只有白点
- 高斯噪声,由于采集器附加的噪声,另一个是由于光学问题带来的噪声。对于高斯噪声就有了这样的假设:首先噪声的产生是相互独立的,而且服从均值为0的正态分布。高斯滤波是一个解决方法
# 高斯卷积
平滑卷积核中权重都是1/9是不合理的,会损失图像的高频信息产生振铃效应(产生了一些水平和竖直方向的条状)。图像处理中,对一幅图像进行滤波处理,若选用的滤波器具有陡峭的变化,则会使滤波图像产生“振铃”,所谓“振铃”,就是指输出图像的灰度剧烈变化处产生的震荡,就好像钟被敲击后产生的空气震荡。
因此需要将卷积核调整的更平滑
二维的高斯函数公式
高斯核里的参数包括:
1窗口大小,
2 б 即方差,决定了周围图像对这个点的影响权重。方差约大,越扁平
得到下面的高斯核 
高斯核总值的和为1
当方差固定时,因为最高点是固定的,所以窗口越小,平滑效果越不明显。因此窗口的大小选择是个经验性的问题,通常为6б +1
两个小高斯核的连续卷积可以用一个大的高斯核代替。
高斯卷积的另外一个特性就是对一副图像进行连续两次б=1的高斯卷积输出结果等价于使用2б的高斯卷积一次的输出结果。
这个满足勾股定理的,比如连续的两次高斯卷积核大小为2б,3б可以使用13б的高斯卷积核代替。
虽然效果一样,但用多个小核会更快
高斯核可分离成两个一维高斯核的乘积,33 的高斯卷积核可以分离出一个13和一个31的一维卷积核,计算结果一致,但可以提高计算效率
拉普拉斯laplacian卷积核 约等于 一个单位脉冲卷积核与一个高斯卷积核相减
# 中值滤波器
上面讲到的都是求滤波器范围内的平均值,属于均值滤波器,对于椒盐噪声处理能力弱


中值滤波器:对滤波器范围内的计算求中间值



