 图像频谱
图像频谱
# 图像频谱
Owner: -QVQ-
# 图像频域滤波
spatial domain(空间域): 数字图像f(x,y)=color为一个定义在二维空间中的矩形区域上的离散函数**。**
frequency domain(频域): 可以将一幅图像的像素值在空间上的变化分解为具有不同的振幅、空间频率和相位的简振函数的线性叠加。图像中各种空间频率成分的组成和分布称为 图像频谱。在频域一些特性比较突出,容易处理
可以通过某些变换手段如(傅里叶变换,离散余弦变换,小波变换等)在频域下对图像进行处理可以将图像由空间域转换到频域。
空间域滤波: 用各种模板直接与图像进行卷积运算
频域滤波: 将空间域上的数字图像变换为频域滤波,进行处理,反变换回空间域
图像的频率:灰度值变化剧烈程度的指标,是灰度在平面空间上的梯度。
图像的**高低频:**灰度缓慢地变化的一块区域。除去高频的就是低频了
高频显示图像边缘、图像的细节、、噪声(即噪点)
# 采样和混叠Sampling and aliasing
采样因子为:扔掉每隔一行和一列来创建1/2大小的图像
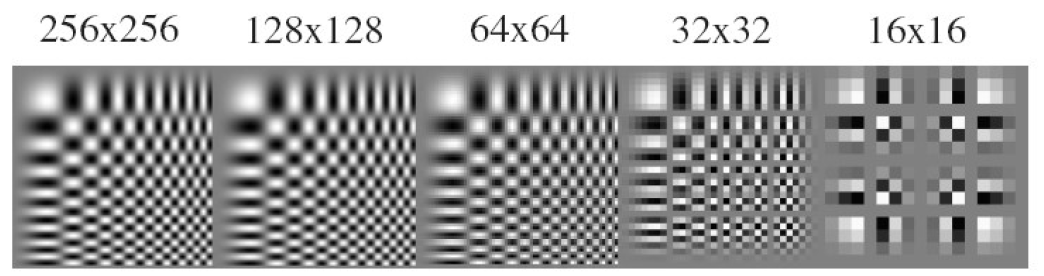
出现的问题:在一维频谱的例子中,会丢失频率的变化信息
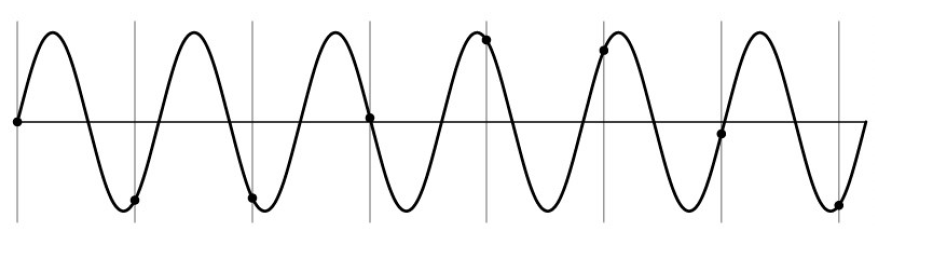
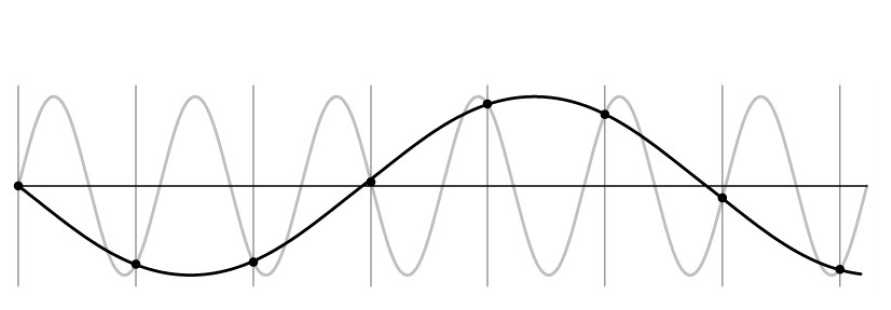
对于具体的图像而言,即丢失纹理信息,产生混叠问题

# 反混叠Anti-aliasing
# Nyquist-Shannon sampling theorem• 奈奎斯特-香农抽样定理
采集离散的信号时,采样频率必须≥ 2 * 最大输入信号频率,这使得我们能完美的重构原始的信号
# 去除新采样频率中大于一半的频率
这将丢失一些信息,但比器混叠会更好,可以再结合平滑滤波器
# **缩减像素采样(**downsampling)因子为2的算法
以下为matlab伪代码
image = im2double(imread('luke.jpg'))#将图像转为浮点型数据结构应用低频滤波器
im_blur = imfilter(image,fspecial('gaussian',7,1))
即对图像使用7*7大小的,方差因子为1的高斯滤波
对每一个点采样
im_small = im_blur(1:2:end,1:2:end )扔掉每隔一行和一列来创建1/2大小的图像
不使用滤波器直接采样:

使用高斯滤波器后采样

# 混合图像Hybrid Images
对于下图,从远处看是人,近处看是猫,为什么我们会对混合图像有依赖于距离的不同理解

从坎贝尔-罗布森对比灵敏度曲线可以得到,中高频的知觉线索主导知觉。
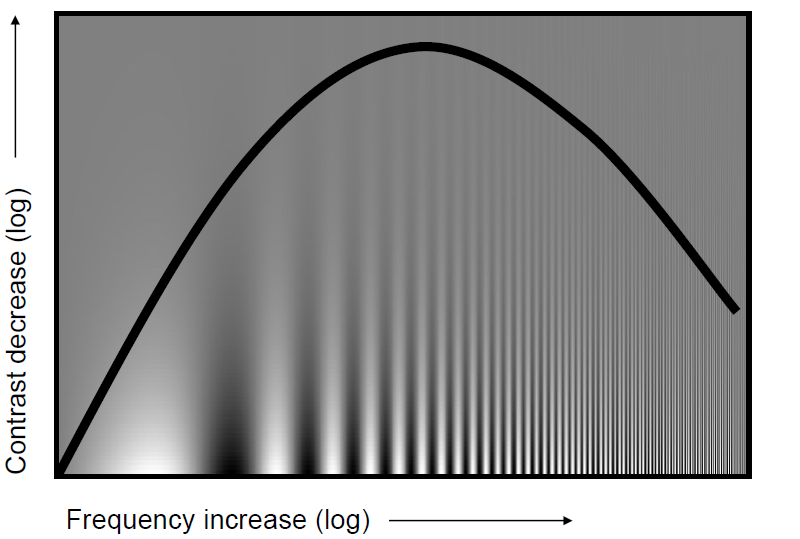
# 傅里叶
# Rolling Shutter: 果冻效应
当使用电子快门来拍摄高速移动的物件时,原本垂直的物件拍摄出的画面却为倾斜甚至变形。

# 傅里叶级数Fourier series
任何函数都能由正弦函数和余弦函数组成
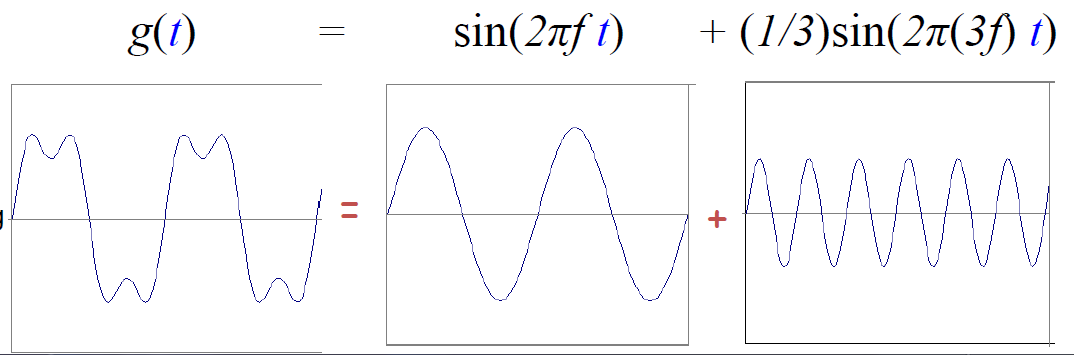
对于图像信号 –图片是二维,公式是一维 –图片数据有限且离散,公式无限且连续 –二维矩阵中每一列(或者每一行)数据都可以单独看作一个波,对一个MxN的矩阵,可以看作N个Mx1的波
二维的分解 –在二维傅立叶变换里,先分别对每一列(行)做傅立叶变换,会得到同样大小的傅立叶系数向量 –再在另一个维度(上面是行这里就是列,上面是列这里就是行)对这些系数做傅立叶变换
# 图像的傅里叶变换
特征:
•距离原点越远=频率越高=原图中灰度值的变化越频繁。 •灰度值越大=幅值越大=原图中灰度值变化的范围越大。
变换:
对于图像信号:将二维矩阵中的每一列数据看成一个波,MN个矩阵看成N个M1的波
二维的分解:先对每一列作傅里叶变换,得到同样大小的傅里叶系数向量,再对每一行作变换
图片的 像素值:

ω是所有频率波的单位频率,决定了波叠加的效果
f(x)可以看成是P个频率的正弦和余弦波的叠加
对一个图片,其中一列数据( N x 1的向量),把这列数据看作是周期为N的周期数据
求出𝑎𝑛和𝑏𝑛的值,即求出这些振幅的具体数值,就完成了图像的离散傅里叶变换
一列图像大小为N*1,则未知数有2P+1个
通过傅里叶变换转为时域图,对其统计频率的高点得到频谱图
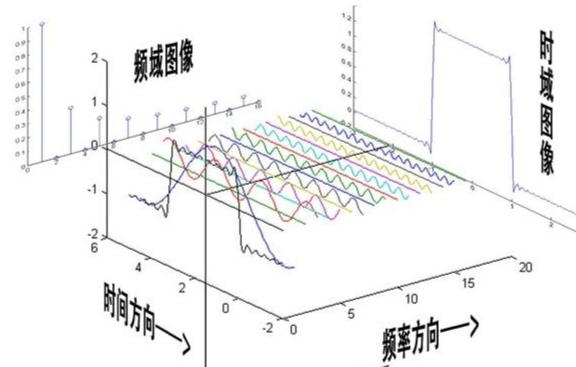
Spatial domain时域图像:反应了不同时间的频率,在图中黑色部分为所有频率累加后得到的图像
Frequency domain频域图像:频率方向总是从左到右为从高频到低频的,反应了图像在各列变化的最大值。横轴为频率,纵轴为振幅。
相位图:
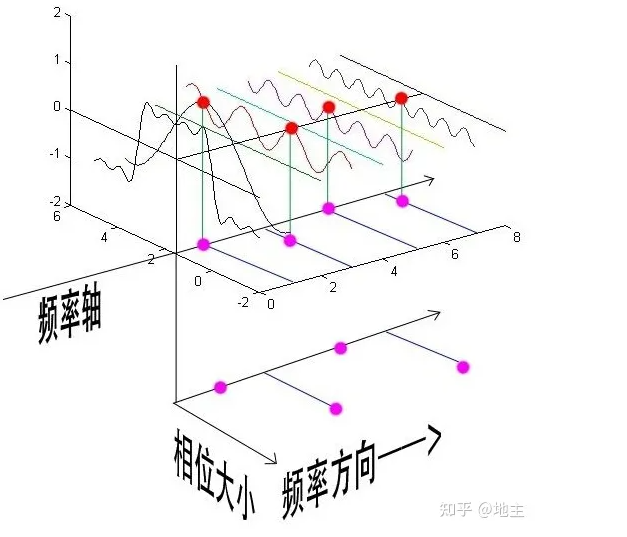
# 频谱图Amplitude
–用来代表这个频率波的振幅大小 –一个N x 1的信号,其由𝑵−𝟏𝟐个频率的波叠加,计算所得数据左右上下对称
频谱图上每一个点均代表一个固定频率、幅值、相位的正弦波图像,那么抛开频谱图上幅值为0 的点外,其他的所有点都映射着一张正弦图。
将图像转化为时域再转化为频域图
当n=1,2,…N时,c𝐧和𝒄𝑵−𝒏共轭对称
越靠近坐标角落,频率越低
便于观察,互换角落和图片中心位置的数值

我们看到频谱图中心代表的是低频,往四面八方扩展后逐渐变为高频,并且左上-右下、右上-左下完全对称。其中黑色部分即表明该图像不含有该部分的频率,相反颜色越亮,该频率的幅值越高。通常中心处是最亮的,即低频信号是最多的,这也和原时域图的信息是匹配的。
把所有的正弦图(F(w))叠加在一起,便能够恢复出原始的时域图,进一步得到原图
右边这张图,假设频谱图中有1000个值不为0 的亮点,那么它们会生成1000张固定频率、幅值和相位的正弦图像,把这一千张图像加在一起(包括基底的图),我们就能得到左边的原图。

下面举几个例子来理解频谱图:

纯黑图是一样的,其他纯色图只有中心有一个白点
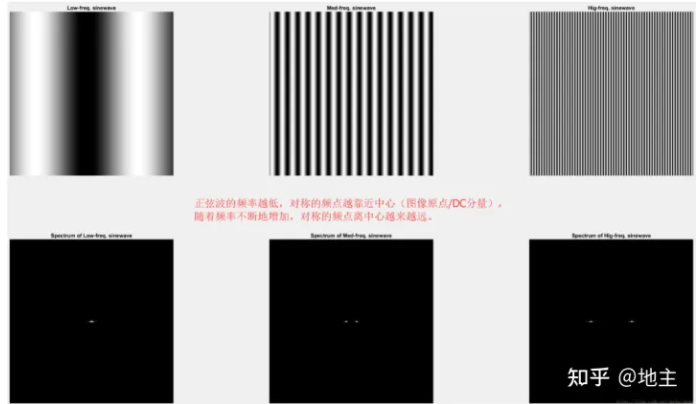
- 只有2个点(对称关系,实则即1个点)
- 靠近中心,频率低,靠近边缘频率高
- 亮点在频谱图的x方向上,与时域图正弦分布的方向一致
- 基底为0,对应于时域图的平均亮度也为0
如果频谱图上的点相对于中心点有一定角度,对应的时域正弦图像也有一定的角度

平移不改变频谱


# 频谱图Amplitude的意义
下图为原图得到频谱图

下图为我们将低频信号的幅值变为0后的时域-频域图
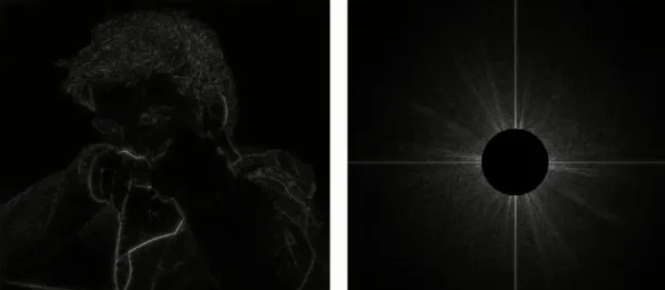
下图为保留低频信息,滤除高频信息的图。

一些滤波器也能起到同样的效果。滤波器本质上也是去掉高频或者低频的信息。但在频域里得到这样的图片,比在时域里去对图像做变换要简单的多

对于上图的匹配。
图1高频没有,只有低频出现,即变换趋势很小,图D符合
图2各个方向低频高频都很平均,和图5的区别就是图5斜方向的低频少,所以对应图B
图3是对称的,因此实际上只有一个点,即低频没有,中频居多
图4垂直方向有高频,水平方向高频少,对应图E水纹垂直方向亮度变换大,水平方向变换小
图5正水平和正垂直方向有高频,其他方向高频少,对应图C
# 其他
相位是指一个波的起始点在其周期内的位置。相位信息是指在信号中各个频率分量所占的相位差异。在傅里叶变换中,相位信息是指每个频率分量上的相位角度,可以用相位图表示。
相位信息对于恢复原始信号非常重要,因为在傅里叶变换中,振幅和相位是分开计算的,振幅信息存储在频谱图中,而相位信息存储在相位图Phase中。因此,只有同时获取到振幅和相位信息,才能完全恢复原始信号。
人眼对于图像的识别,相位图的信息起了注意作用。
反卷积是很难的,即使已知用的是哪一个滤波器


